Projects

Project 1: Exact 1D Reduction Models for Complex Dynamics in Non-Normal Networks



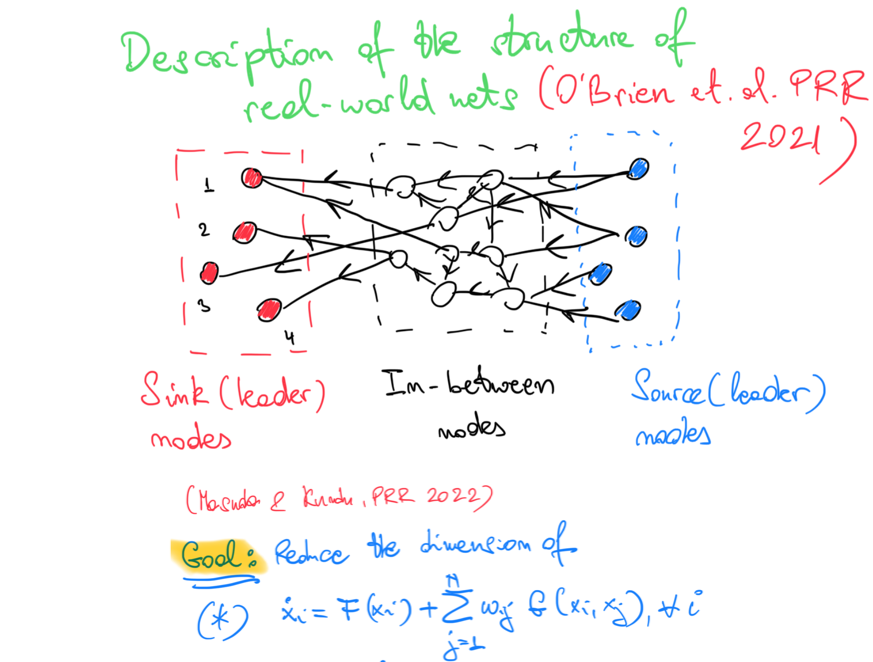
Project Image

This project focuses on the study of complex systems represented by real-world non-normal networks, characterized by strong directedness and structural asymmetry. Both non-normal networks and the critical role of source nodes were first discovered by the PI and collaborators, unveiling a new paradigm in understanding the structure and dynamics of complex systems. Non-normal networks are distinct in that their adjacency matrices exhibit non-normality, where $(AA^T \neq A^T A)$. Source nodes, which play a pivotal role in these systems, act as sinks or sources of information, inducing transient growth that significantly influences emergent behaviors. This project is conducted in collaboration with Prof. Naoki Masuda from the University of Buffalo, further enhancing the exploration of these phenomena.

The primary goal of this project is to develop a rigorous, systematic approach to reducing the dimensionality of non-normal networks into 1D models, while preserving essential dynamical behaviors, particularly near critical phenomena like phase transitions. Non-normal networks, widely observed in neural systems, ecological interactions, and social structures, challenge conventional network theory with their directed edges and hierarchical properties. Recent research led by the PI has further demonstrated the ubiquity of non-normal networks in real-world datasets, showcasing their hierarchical organization and the role of source nodes as key drivers of system dynamics.

By leveraging asymptotic expansions and exploiting the spectral properties unique to non-normal networks, we aim to demonstrate that these 1D reduction models are exact for networks dominated by source nodes. This reduction will simplify mathematical analysis, enhance computational efficiency, and allow for accurate modeling of complex systems with minimal loss of critical dynamical features. These reductions are particularly important in capturing emergent dynamics near phase transitions, where conventional methods often fall short.

Ultimately, this project will reveal how non-normal networks, driven by the influence of source nodes, naturally lend themselves to precise reductions, enabling a deeper understanding of stability, robustness, and collective behaviors in complex systems. The insights gained will have broad applications, from computational neuroscience to ecosystem modeling, offering new avenues for studying the dynamics of large-scale interconnected systems.

Papers:





Project 2: Diffusion in Heterogeneous Media Through Nonlinear Random Walks: Optimizing Li+ Battery Design



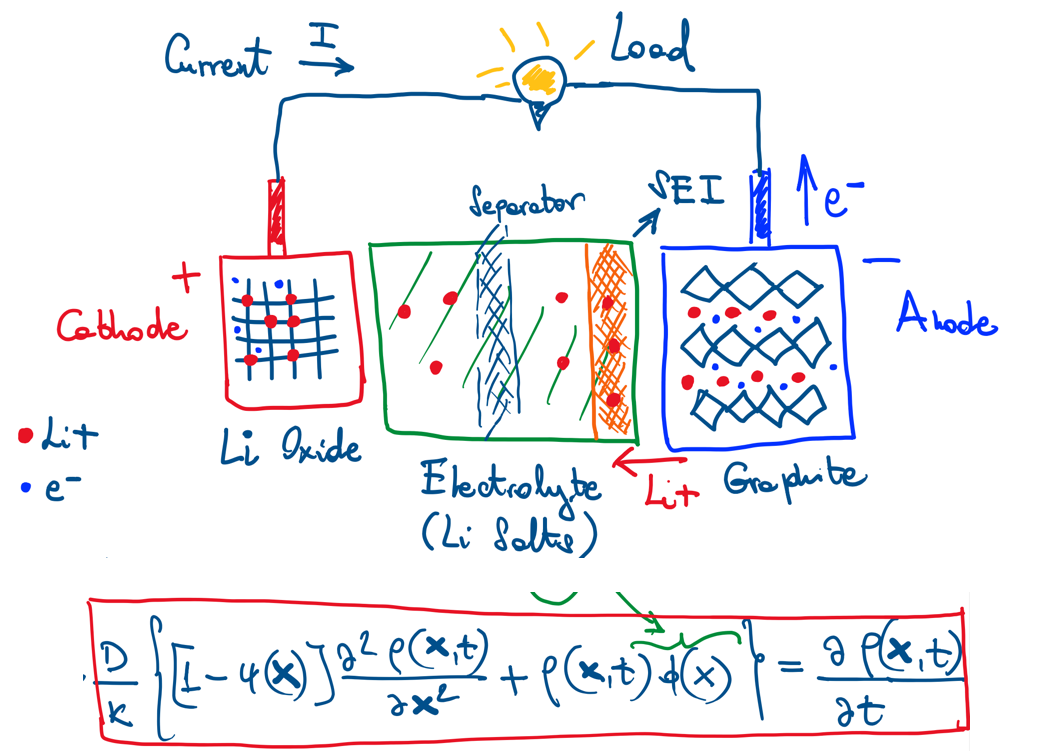
Project Image

This project focuses on maximizing the lifetime of Li+ batteries by utilizing nonlinear random walk models, developed by the PI, based on a microscopic description using the master equation and asymmetric volume-excluded processes. In the first stage, averaging methods will be used to derive the mean-field equations, which take the form of partial differential equations (PDEs), modeling diffusion in highly heterogeneous media where traditional homogenization methods fail due to the absence of spatial periodicity. Perturbation methods will be applied to verify the abnormal diffusion behavior observed in such systems.

In the second stage, this mathematical framework will be applied to Li+ batteries, examining how diffusion processes influence battery lifetime, particularly by investigating how Li+ ions become trapped during repeated charging and discharging cycles, which reduces battery efficiency over time.

In the final stage, a machine learning framework will be developed to optimize the design of the battery medium, aiming to extend battery lifetime by minimizing the immobilization of Li+ ions through improved material and structural design.

Papers





Project 3: Structure and Dynamics of Non-Normal Networks



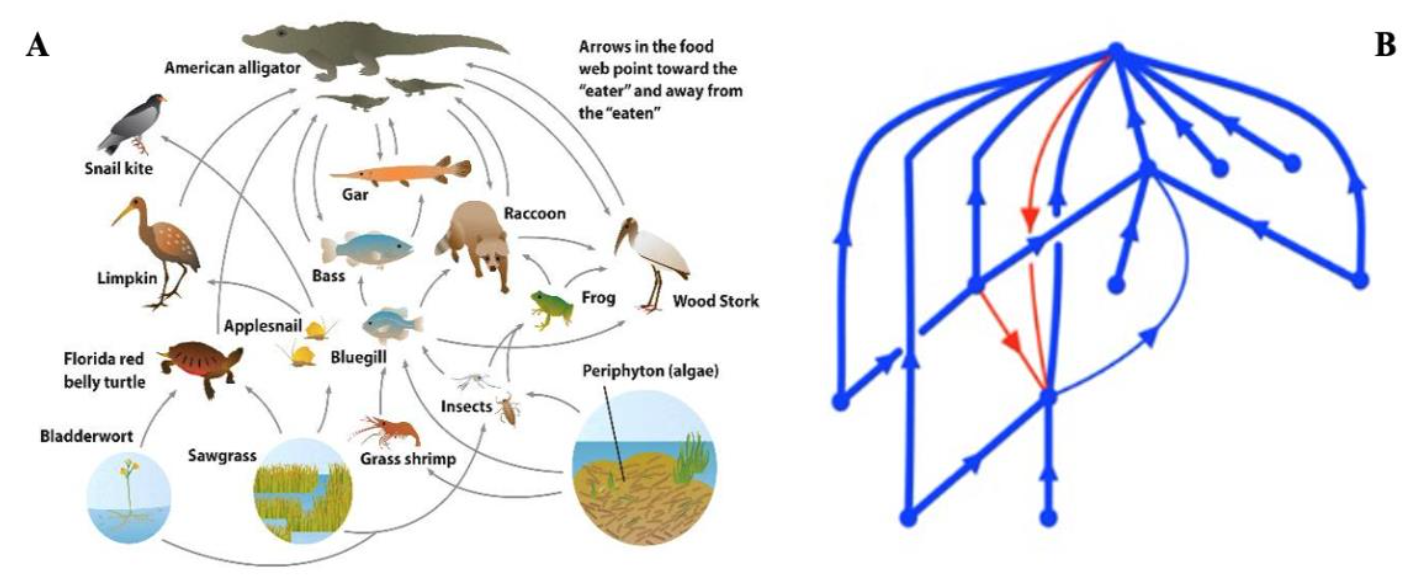
Project Image

This project delves into the complex behavior of non-normal networks, focusing on the intricate interplay between network structure and dynamics. Non-normal networks, recently introduced by the PI and collaborators, are directed networks characterized by their non-symmetric adjacency matrices, where $( A^T A \neq AA^T )$. These networks, which are ubiquitous in real-world systems ranging from biological networks (neuronal, genetic, ecological) to human-made ones (social, economic, and communication networks), exhibit unique structural features such as localization and spectral clustering.

Localization refers to the concentration of network dynamics in specific regions, where certain nodes accumulate mass or activity, leading to focused and localized behaviors. On the other hand, spectral clustering reflects the emergence of densely connected groups of nodes that exhibit synchronized or clustered activity patterns. Together, these structural phenomena are key to understanding how network topology influences dynamic processes such as synchronization, pattern formation, and robustness in complex systems.

The project explores how these structural properties—localization and clustering—impact the collective dynamics of non-normal networks. Using advanced data science and machine learning tools, the project will analyze large datasets of empirical networks to reveal how hierarchical structures and modularity influence these dynamics. The goal is to uncover how localized eigenvectors, representing concentrated activity in specific network regions, and clustered eigenvectors, indicating closely grouped dynamic behaviors, lead to phenomena such as synchronization robustness, pattern localization, clustered oscillations, and species coexistence in ecological models.

By leveraging symmetry-breaking methods developed by the PI, the project seeks to demonstrate how spectral localization and clustering contribute to the emergence of localized and clustered patterns in non-normal networks. This investigation aims to deepen our understanding of the fundamental principles driving the dynamics of complex systems, particularly the role of hierarchy and modularity in shaping the collective behaviors observed in non-normal networked systems.

Papers





Project 4: Hierarchy and Modularity as Driving Forces for Stability and Diversity in Complex Systems



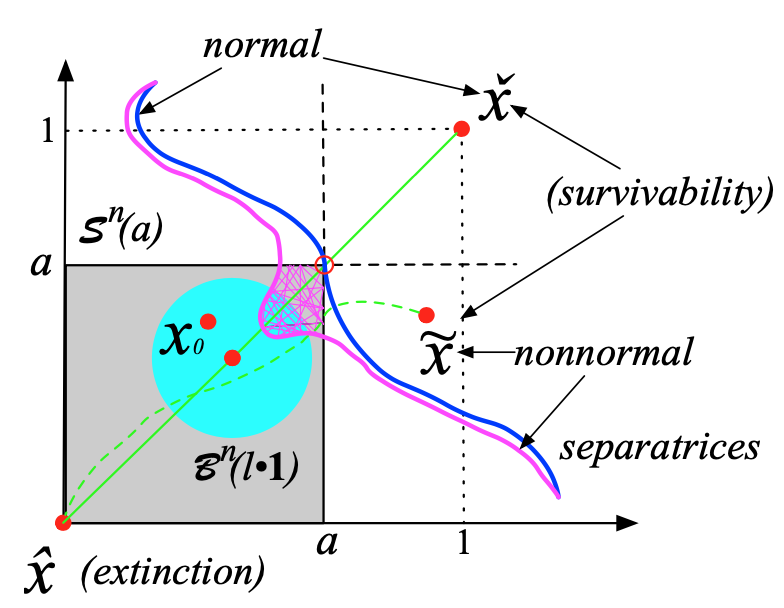
Project Image

This project explores the dual roles of modularity and hierarchy in driving the stability and diversity of complex ecological systems. Herbert Simon famously conjectured that both hierarchy and modularity are crucial to the organization and resilience of complex systems. Recent findings have provided new insights, showing that hierarchy is better represented by non-normality—a property of networks where $( A^T A \neq A A^T )$—rather than modularity alone. Non-normality captures the directed and asymmetric interactions that are widespread in ecological and biological networks, while modularity refers to the segregation of nodes into tightly connected communities.

The project’s central aim is to show how these two structural features—modularity and non-normality—together enhance the robustness of stable states and drive diversity in ecological systems. Modularity enables localized clustering of dynamics within communities, while non-normality induces transient growth and directs the flow of interactions in a hierarchical fashion. These complementary features work together to promote stability, ensuring that ecosystems can withstand disturbances while preserving their diverse species composition.

Using a large dataset of intra-species interaction networks, the project will analyze how non-normality strengthens intra-species cooperation and increases individual survivability. In parallel, we will investigate how modularity promotes self-organization within communities, fostering resilience at different scales of the ecosystem. The structural clustering created by modularity supports stable localized behaviors, while non-normality governs the broader system-wide interactions.

To model these interactions, we will apply a generalized Lotka-Volterra mutualistic model under the Allee effect—a framework that captures bistable dynamics in population models. By integrating these structural insights into this modeling framework, we aim to uncover how modularity and non-normality jointly affect the robustness of stable states, particularly in terms of species coexistence, ecosystem stability, and resilience to environmental perturbations.

Ultimately, this project seeks to validate Simon’s hypothesis on hierarchy and modularity by demonstrating how non-normality and modularity work in tandem to maintain the complex interplay between stability and diversity in natural systems. The findings will offer a new perspective on ecological organization, emphasizing the critical roles of these structural features in the resilience and persistence of ecosystems.

Papers





Project 5: From Random Walk Coupling to Non-Normal Networks: Synchronization in Biochemical and Neural Models



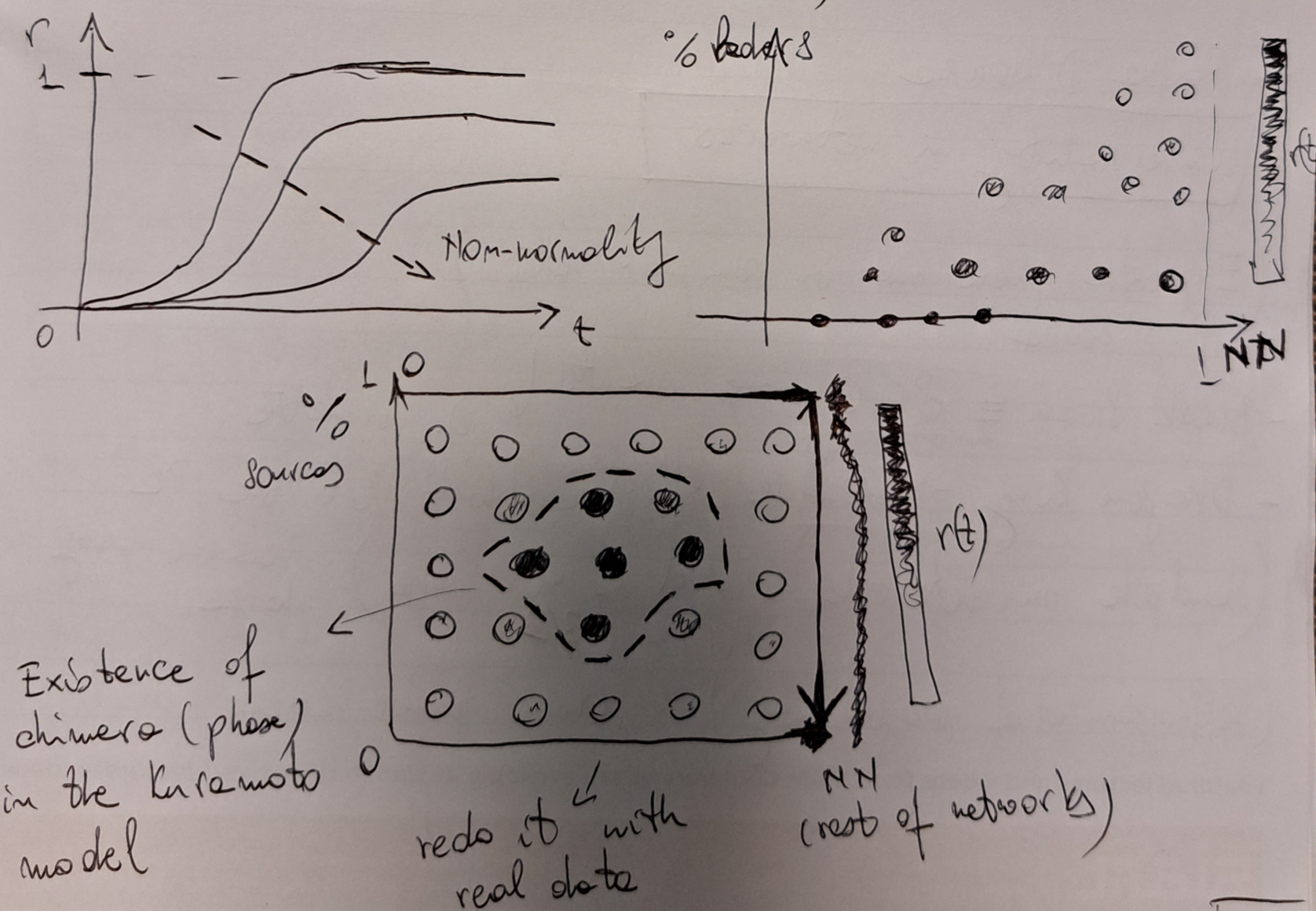
Project Image

This research project investigates synchronization in real-world networks, focusing on biochemical and neural systems. The study begins by modeling interactions through reaction-diffusion dynamics, capturing the spatial and temporal evolution of complex systems. As the complexity increases, these models are reduced to phase-based representations, such as the Kuramoto model, which focuses on oscillator phases. This reduction simplifies the analysis while preserving essential dynamical properties, offering insights into the collective behavior of the system.

The first part of the project explores synchronization through random walk coupling, simulating diffusive processes between network nodes. This approach mirrors how local interactions spread across the network, leading to global synchronization. The diffusive coupling framework helps model processes like molecular interactions in biochemical systems or signal propagation in neural networks, providing insights into how synchronization emerges from local dynamics.

The second part investigates synchronization in non-normal networks, where $AA^T \neq A^TA$, indicating that the adjacency matrix is non-normal. In these networks, the influence between nodes is directional and imbalanced, leading to asymmetric coupling structures. Non-normal networks are omnipresent in real-world systems, including biochemical and neural systems, and often lead to complex synchronization behaviors. The presence of source nodes introduces further asymmetry, enhancing the diversity of possible synchronization patterns. By studying non-normal coupling, this research aims to uncover the role of network topology in facilitating or inhibiting synchronization.

Using slow-fast perturbation methods and spectral techniques, the study will analyze how random walks and non-normal networks contribute to global synchronization, cluster synchronization, and the formation of chimera states, where synchronized and unsynchronized regions coexist within the same network.

Papers