Research
My research explores the intricate and fascinating nonlinear phenomena that emerge in biological, ecological, and physical systems, with a growing emphasis on data science applications. By combining tools from dynamical systems, spectral graph theory, probability, and numerical analysis, I investigate how complex, coupled systems exhibit self-organizing behaviors, such as synchronization, pattern formation, and diffusion processes. A key aspect of my work involves uncovering the hidden structures within natural systems and analyzing how these structures give rise to collective, emergent dynamics. My research spans diverse areas, including ecosystem stability, species diversity, computational neuroscience, and the dynamics of social systems, offering fresh insights into the interconnectedness and resilience of these systems.
My current active research directions are:
Emergent Phenomena
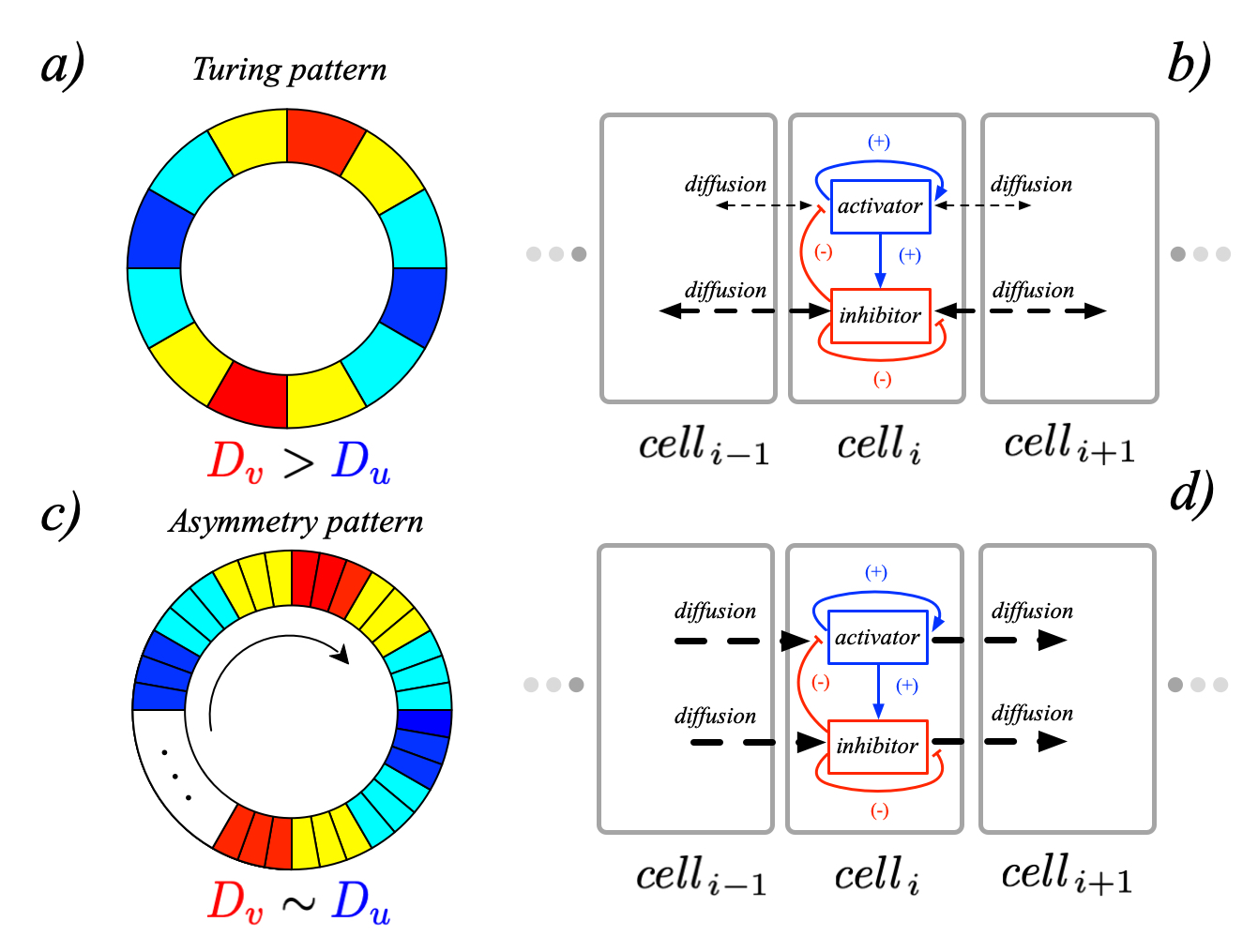
Since my Ph.D., I have devoted part of my research efforts to the problem of pattern formation for reaction-diffusion models based on networked systems.
-
With D. Fanelli and T. Carletti, I have shown that spatial patterns can spontaneously develop due to the unique topological organization (directed [1], multi-layered [2], Cartesian [3], anisotropic [4], and multigraph [5] of biological/ecological complex networks.
-
I have developed a new class of instabilities, termed topology driven, for reaction-diffusion models on directed networks [1]. It can be rigorously proven that a directed network (e.g., brain network) can firmly relax the Turing conditions for the formation of patterns.
-
We have also studied the effect that time delays have on the pattern formation process [6, 7]. In particular, proving the possibility of pattern forming in a single species system.
-
Also, with D. Fanelli, I have studied the emergence of macroscopic self-organization patterns that develop via a resonant amplification of the stochastic noise, which stems from finite-size fluctuations [8, 9, 10].
-
With P.K. Maini, I have explored the role of asymmetric diffusion in multicellular tissues in solving the Turing paradox and establishing asymmetric diffusion of morphogens, periodic boundary conditions, and the size of the multicellular system as key factors [11].
-
During B. A. Siebert's Ph.D. thesis, we proved that neuronal networks’ modularity shapes patterns of brain activity [11]. With J.P. Gleeson and A. Arenas, we have used a symmetry-breaking mechanism to explain the emergence of the chimera states [12].
References
- The theory of pattern formation on directed networks
- Turing patterns in multiplex networks
- Turing instabilities on Cartesian product networks
- Pattern formation for reactive species undergoing anisotropic diffusion
- Tune the topology to create or destroy patterns
- Pattern formation in a two-component reaction–diffusion system with delayed processes on a network
- Delay-induced Turing-like waves for one-species reaction-diffusion model on a network
- Stochastic amplification of spatial modes in a system with one diffusing species
- The linear noise approximation for reaction-diffusion systems on networks
- Stochastic Turing patterns on a network
- Role of modularity in self-organization dynamics in biological networks
- Symmetry-breaking mechanism for the formation of cluster chimera patterns
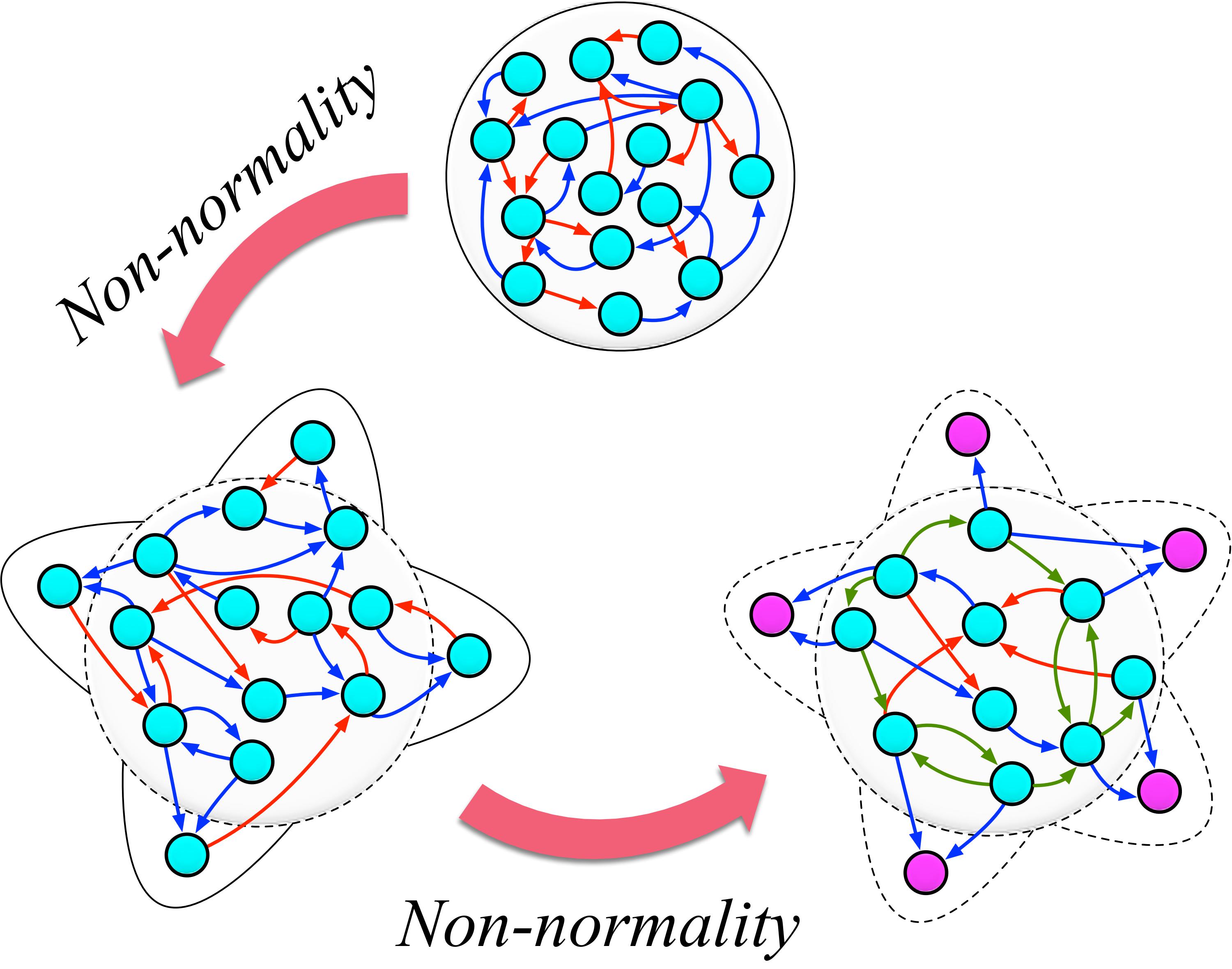
Non-normal networks
Non-normal networks, a new paradigmatic concept that I have recently introduced [1, 2, 3, 4, 5, 6], the ubiquity in the real world, ranging from biological/ecological networks (neuronal, genetic, metabolic, proteins, food webs) to human-made networks (social media, scientific citations, transport, communications).
-
An immediate consequence of non-normality is a transient growth observed in the linear regime of stable non-normal networks. With T. Carletti and R. Lambiotte, I have shown that this particular property can strongly impact all kinds of nonlinear phenomena, which at first order can be described by the Master Stability Function (MSF) [2, 5], thus making many of the classical spectral methods to fail.
-
I have also illustrated the role of non-normal networks in ecology concerning species diversity and their coexistence in a competitive environment, including the Allee effect, which strongly depends on the trophic’s non-normal nature relations [2, 3]. We have recently shown that the non-normality of real complex systems can be a suitable new mechanism for emergent self-organization beyond the Turing instability [3, 4].
-
On the other hand, it can be an 'ad hoc' instrument for amplifying demographic fluctuations, which can eventually induce a new dynamical behavior [5]. This way, non-normality further strengthens the role of the finite-size effect in spatial patterning.
-
Furthermore, with J.D. O’Brien and K.A. Oliveira, we show that in the ensemble of real-world networks, when some given level of non-normality is reached, leader nodes (with only incoming or outgoing degrees) simultaneously emerge [6].
References
- Topological resilience in non-normal networked systems
- Structure and dynamical behavior of non-normal networks
- Patterns of non-normality in networked systems
- Resilience for stochastic systems interacting via a quasi-degenerate network
- Synchronization Dynamics in Non-Normal Networks: The Trade-Off for Optimality
- Hierarchical route to the emergence of leader nodes in real-world networks
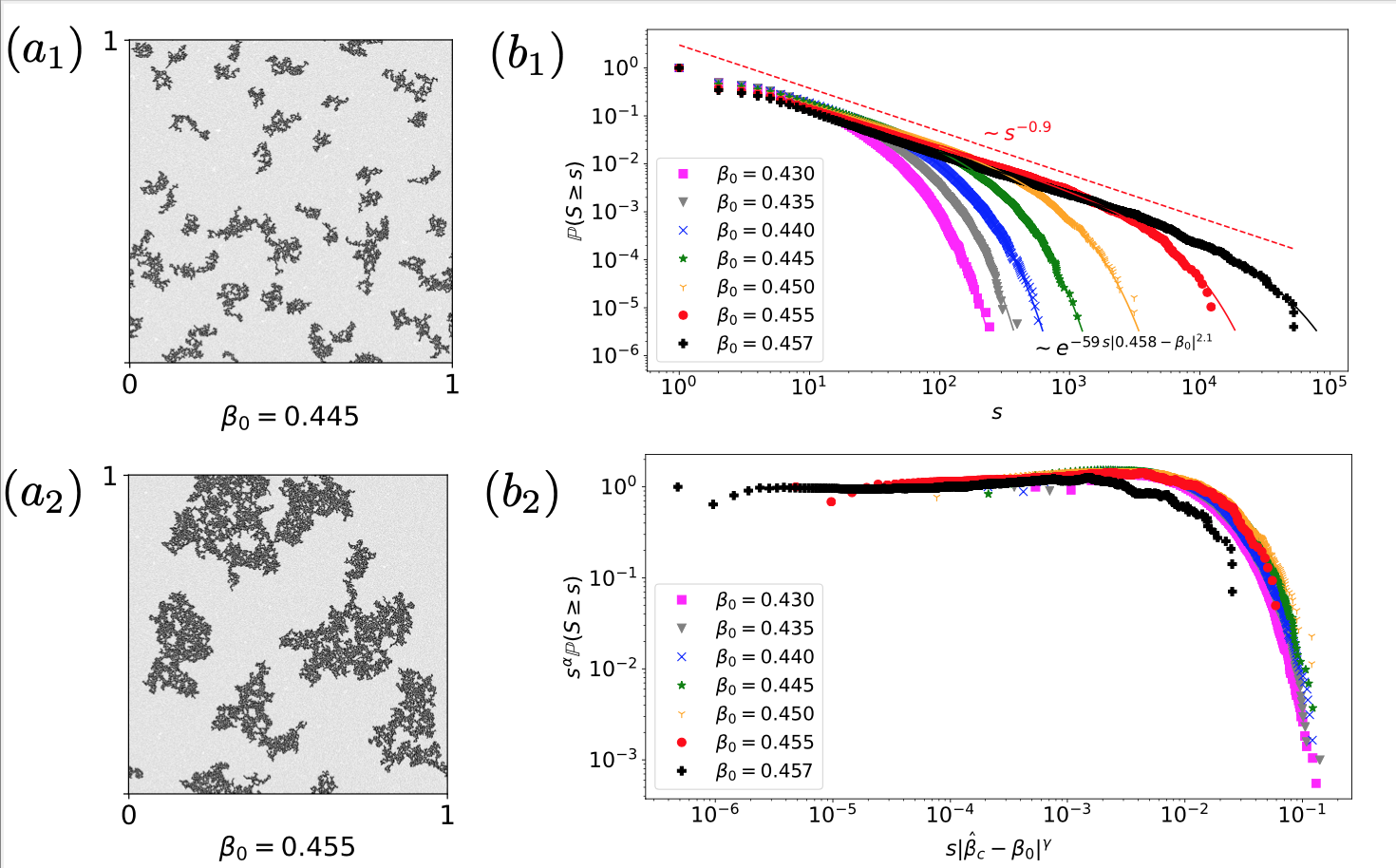
Nonlinear random walks
The finite-size-based description of the dynamical processes of networked systems captures structural features that are not possible to be detected otherwise. In this direction, I have formulated the nonlinear random walk diffusion process on a network when the nodes’ finite carrying capacities are taken into account.
-
Such nonlinear random walks allow the construction of inverse problems by reconstructing the degree distribution and the total number of nodes of the network based on a set of successive observations from a single (randomly chosen) node [1].
-
Furthermore, with V. Latora, we have proven that such nonlinear random walk processes contribute to optimal spatial support exploration, quantified by an entropy rate measure [2].
-
In the same direction, with J.P. Gleeson and E. Estrada, I have shown that the interplay of dynamics between the node-based and the global network makes impossible the full determination of the network structure [3].
-
In B.A. Siebert's Ph.D. thesis, we have introduced the ESIR epidemic model. Based on nonlinear random walks, such a model optimizes the trade-off between costs and prevention in epidemics lockdowns [4].
-
As part of J.-F. de Kemmeter's Ph.D. project, we show that a nonlinear diffusion process on a heterogeneous landscape can yield a self-segregation process and explain the emergence of vacant habitats (niches) [5].
References
- Hopping in the Crowd to Unveil Network Topology
- Nonlinear walkers and efficient exploration of congested networks
- Dynamics impose limits to detectability of network structure
- Nonlinear random walks optimize the trade-off between cost and prevention in epidemics lockdown measures: The ESIR model
- Synchronization Dynamics in Non-Normal Networks: The Trade-Off for Optimality
- Self-segregation in heterogeneous metapopulation landscapes
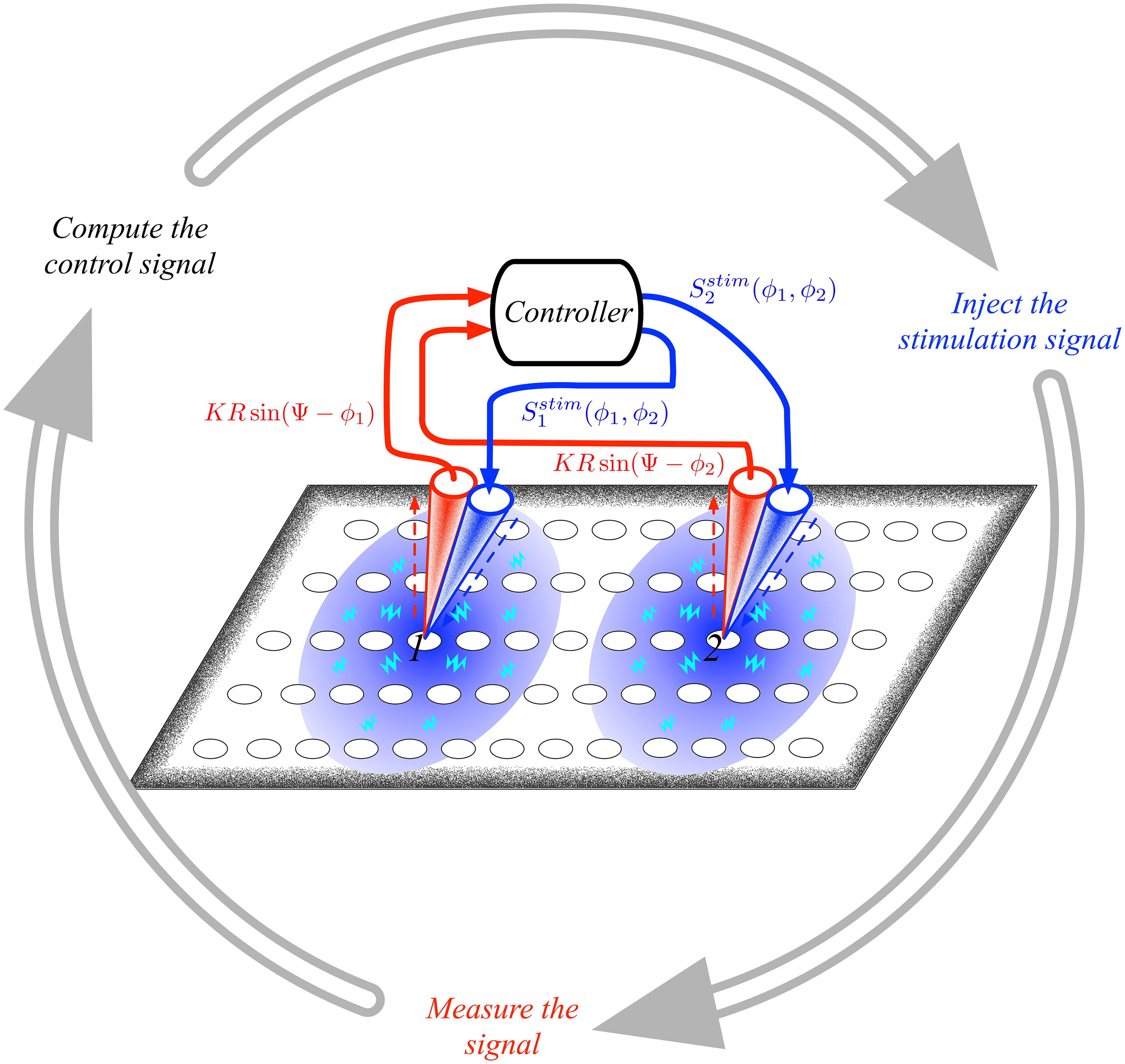
Control-Driven Neurostimulation
I study the control of synchronization dynamics of coupling oscillators (e.g., neurons) with applications to computational neuroscience such as the control of symptoms in neurodegenerative diseases such as Parkinson’s, epilepsy, or compulsive-obsessive disorder.
-
I have introduced a desynchronization method [1], which uses a Hamiltonian formulation of the Kuramoto model, a well-known paradigmatic model for describing the collective dynamics of phase-coupled oscillators.
-
Based on the method above, I have developed a control protocol that minimizes the invasiveness of the Deep Brain Neurostimulation technique by controlling the symptoms caused by the abnormal synchronization at either the basal ganglia or cortex level [2].